День 3: Haskell путеводитель по нейронным сетям
После того как мы посмотрели, как работает сеть, стало ясно, что понимание градиента жизненно необходимо. Отсюда, пересмотрим нашу стратегию на уровне ниже. Однако, так как нейронные сети становятся сложнее, вычисления градиента в ручном режиме становится еще тем делом. Но всё еще есть выход! Я очень рад, что сегодня мы наконец познакомимся автоматической дифференциацией, естественным инструментом в изучении арсенала глубокого обучнеия. Эта статья написана под впечатлением от Hacker's guide to Neural Networks. Для сравнения так же стоит посмотреть Python версию.
Почему случайный локальный поиск не подходит
Следуя инструкции от Картпатого, для начала рассмотрим простую цепь умножений. Haskell не Javascript, поэтому перепишем явным образом.
forwardMultiplyGate = (*)
Or we could have written
forwardMultiplyGate x y = x * y
чтобы сделать функцию более понятной f(x,y)=x⋅y. В любом случае,
forwardMultiplyGate (-2) 3
Возвращает -6. Отлично!
Теперь вопрос: есть ли возможность изменить (x,y) чтобы улучшить вывод? Один из способов это произвести локальный случайный поиск.
_search tweakAmount (x, y, bestOut) = do
x_try <- (x + ). (tweakAmount *) <$> randomDouble
y_try <- (y + ). (tweakAmount *) <$> randomDouble
let out = forwardMultiplyGate x_try y_try
return $ if out > bestOut
then (x_try, y_try, out)
else (x, y, bestOut)
Не удивительно, функция выше отражает простую итерацию цикла for. Что он делает: случайным образом выбирает точки вокруг начальных (x,y) и проверяет увеличился ли вывод. Если да, тогда он обновляет лучшие известные входные и максимальные выходные данные. Чтобы пройтись по значениям, мы можем использовать foldM :: (b -> a -> IO b) -> b -> [a] -> IO b. Эта фукнция удобна так как ожидаем взаимодействие с "реальным миром" в виде случайно сгенерированных чисел.
localSearch tweakAmount (x0, y0, out0) =
foldM (searchStep tweakAmount) (x0, y0, out0) [1..100]
Код говорит нам, что мы наполняем код с какими-то начальными значениями x0, y0 и out0 и проходимся от 1 до 100. Ядро алгоритма - searchStep
What the code essentially tells us is that we seed the algorithm with some initial values of x0, y0, and out0 and iterate from 1 till 100. The core of the algorithm is searchStep:
searchStep ta xyz _ = _search ta xyz
что есть довольно удобная функция, которая склеивает 2 части вместе. Она просто игнорирует итерационные числа и вызывает _search. Теперь, нам нужно случайное число в промежутке [-1; 1). Из документации, мы знаем, что randomIO производит числа между 0 и 1. Проскалируем его умножая на 2 и вычитая 1.
randomDouble :: IO Double
randomDouble = subtract 1. (*2) <$> randomIO
Функция <$> это синоним fmap. Она применяет чистую функцию substract 1. (*2) тип которой Double-Double ко "внешнему" действию randomIO, тип которой IO Double (yes, IO = input/output)1.
Хитрость для числа минус бесконечность:
inf_ = -1.0 / 0
Теперь запускаем localSearch 0.01 (-2, 3, inf_) несколько раз:
(-1.7887454910045664,2.910160042416705,-5.205535653974539)
(-1.7912166830200635,2.89808308735154,-5.19109477484237)
(-1.8216809458018006,2.8372869694452523,-5.168631610010152)
На деле мы видим как вывод изменился с -6 до -5.2. Но улучшение только 0.008 едениц на итерацию. Это очень не эффективный метод. Проблема со случайным поиском в том, что каждый раз он пытается изменить входные данные в случайных направлениях. Если алгоритм делает ошибку, он должен сбросить результат и начать с последней лучшей позиции. Не правда ли лучше было бы, если вместо каждой итерации результат улучшался пусть даже по чуть чуть но постоянно и не приходилось откатываться?
Автоматическое дифференцирование
Вместо случайного поиска в случайном направлении, мы можем использовать точное направление и количество для изменения входных данных таким образом, чтобы улучшался вывод. И это то что градиент нам говорит. Вместо ручного вычисления градиента каждый раз, мы можем использовать умный алгоритм. Есть можноество подходов: цифровой, символический и автоматическое дифференцирование. В этой статье, Доминик Стейнтц объясняет разницу между ними. Последений подход, автоматическое дифференцирование, именно то что нам нужно: точные градиенты с мнимальным количеством переработок. Кратко поясним идею.
За идеей автоматического дифференцирования стоит ясно определенный градиент только для простых базовых операторов. Затем, мы составляем цепь правил комбинируя операторы в нейронную сеть как хотим. Такая стратегия будет влиять на сам градиент. Давайте посмотрим на метод через пример.
Ниже можно посмотреть оператор умножения и его градиент используя правило.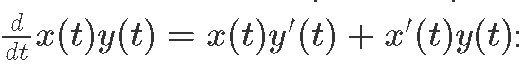 
(x, x') *. (y, y') = (x * y, x * y' + x' * y)
Тоже самое можно сделать со сложением, вычитанием, делением и экспонентой:
(x, x') +. (y, y') = (x + y, x' + y')
x -. y = x +. (negate1 y)
negate1 (x, x') = (negate x, negate x')
(x, x') /. (y, y') = (x / y, (y * x' - x * y') / y^2)
exp1 (x, x') = (exp x, x' * exp x)
Мы так же имеем constOp для констант:
constOp :: Double -> (Double,Double)
constOp x = (x, 0.0)
Наконец, мы можем определить наш любимый сигмоид σ(x) объединяя те операторы, что были выше:
sigmoid1 x = constOp 1 /. (constOp 1 +. exp1 (negate1 x))
теперь давайте посчитаем нейрон f(x,y)=σ(ax+by+c), где x и y это ввод а a, b и c паарметры.
neuron1 [a, b, c, x, y] = sigmoid1 ((a *. x) +. (b *. y) +. c)
Теперь можно получить градиент для a в точке (a=1, b=2, c=−3, x=−1, y=3)
abcxy1 :: [(Double, Double)]
abcxy1 = [(1, 1), (2, 0), (-3, 0), (-1, 0), (3, 0)]
neuron1 abcxy1
(0.8807970779778823,-0.1049935854035065)
Вотт первый пример результата вывода нейронно йсети и второй градиент относительно a 
Проверим математику результата:
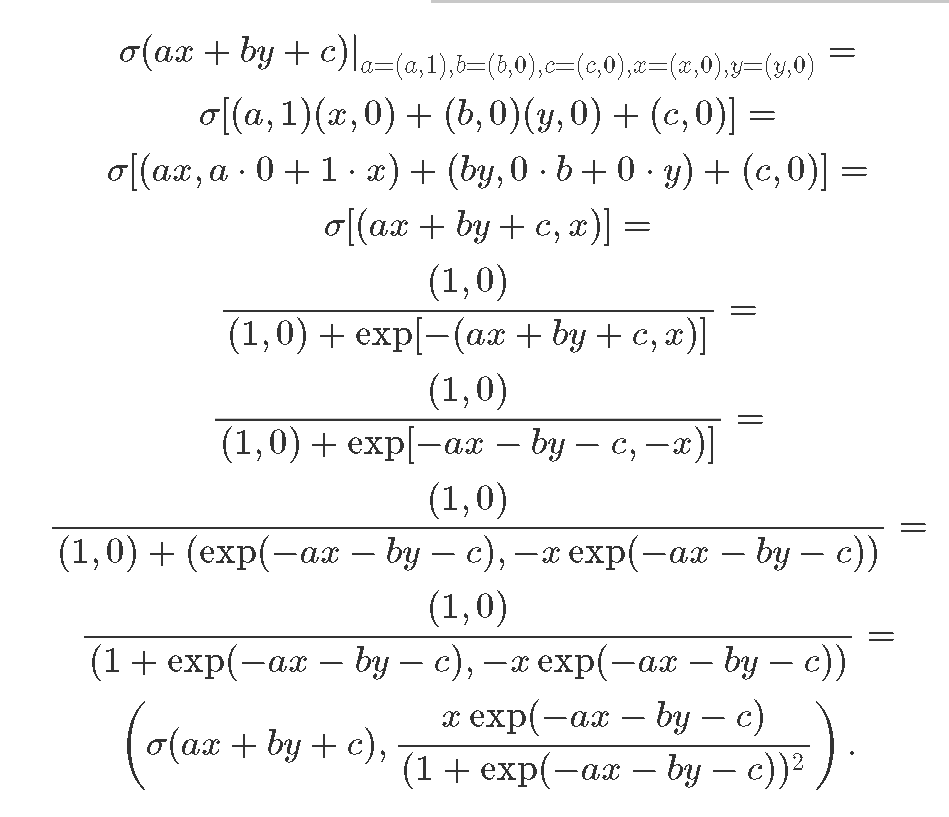Первое выражение это результат вычислений нейронов, а второй точное аналитическое выражение
Вот и вся магия за словами автоматическая дифференциация. Похожим образом, мы можем получить остаток градиента: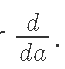
neuron1 [(1, 0), (2, 1), (-3, 0), (-1, 0), (3, 0)]
(0.8807970779778823,0.3149807562105195)
neuron1 [(1, 0), (2, 0), (-3, 1), (-1, 0), (3, 0)]
(0.8807970779778823,0.1049935854035065)
neuron1 [(1, 0), (2, 0), (-3, 0), (-1, 1), (3, 0)]
(0.8807970779778823,0.1049935854035065)
neuron1 [(1, 0), (2, 0), (-3, 0), (-1, 0), (3, 1)]
(0.8807970779778823,0.209987170807013)
Введение библиотеки обратного распределения
Библиотека обратного распределения была написана специально для дифференциального программирования. Она предоставляет комбинаторов для уменьшения нашей головной боли. В добавок, самые полезные операции арфиметические и тригонометрические, уже были определены в библиотеке. Можно взглянуть на hmatrix-backprop для линейной алгебры. Всё что вам нужно для дифференциального программирования определить несколько функций:
neuron
:: Reifies s W
=> [BVar s Double] -> BVar s Double
neuron [a, b, c, x, y] = sigmoid (a * x + b * y + c)
sigmoid x = 1 / (1 + exp (-x))
Тут BVar обернут в маркер того, что функция дифференцируемая.
forwardNeuron = BP.evalBP (neuron. BP.sequenceVar)
Используем изоморфимз sequenceVar для преобразования BVar список в список BVarов, как того требует выражение neuron. И передаем дальше.
backwardNeuron = BP.gradBP (neuron. BP.sequenceVar)
abcxy0 :: [Double]
abcxy0 = [1, 2, (-3), (-1), 3]
forwardNeuron abcxy0
-- 0.8807970779778823
backwardNeuron abcxy0
-- [-0.1049935854035065,0.3149807562105195,0.1049935854035065,0.1049935854035065,0.209987170807013]
Заметим, что все градиенты в одном списке, тип аргумента первого нейрона.
Выводы
Современная нейронная сеть тяготеет к сложности. Написание градент обратного распределения в ручну может легко стать ужасом. В этом посте мы посмотрели как можно автоматизировать этот процесс при надобности.
В следующем посту мы применим автоматическую дифференциацию к реальной сетке. Поговорим о нормализации, других важных методахв глубоком обучении. И затронем сверточные нейнонные сети, котороые помогут нам решить интересные задачи.
Что можно почитать.
Графический путеводитель по нейронным сетям