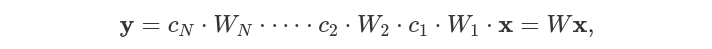День 2: Что делают скрытые уровни?

На прошлом дне, мы ввели понятие обучения одноуровней нейронной сети. Сегодня мы узнаем преимущества многослойной нейронной сети, как правильно её организовывать и обучать.

Когда я обсуждаю нейронную сетку со студентами, которые только начали открывать технику машшиног обучения:

-Я сделал сетку распознавания цифр рукописного ввода. Но моя точность всего лишь Y

-Кажется это горазно меньше чем последнее слово техники, - размышляю я.

-Вот именно. Может быть прроблема в X?

Обычно X это не причина. Реальная причина должна быть более простая: вместо многослойной нейронной сети студент сделал однослойную нейронную сетку или её эквивалент. Эта сеть работает как линейный классификатор, следовательно она не может выучить не ленейные отношения между входом и желаемым выводом.

Так что такое многослойная нейронная сеть и как избежать ловушки с линейной классификацией.

Многослойная нейронная сеть.

Многослойная нейронная сеть, может быть описана как: где x и y это входные и выходные векторы соответственно, - веса матриц и смещение векторов, и 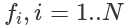функции активации в i'том слое. Нелинейная функция активации f применяется поэлемментно.

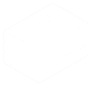
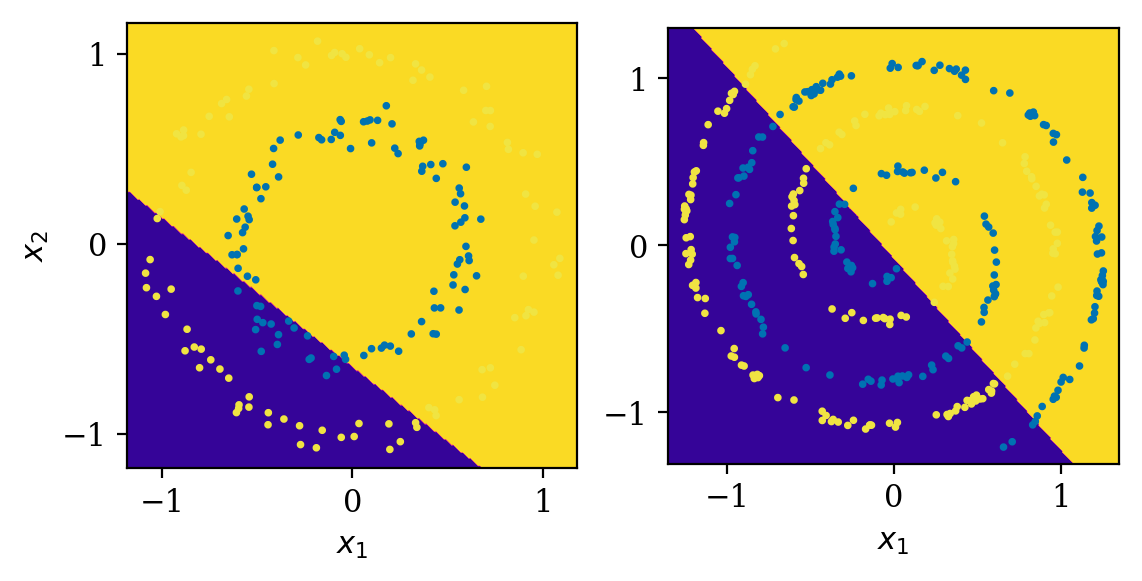
В качестве примера мы сегодня будем использовать двумерный набор данных как показано ниже.

Оба набора свойств двху классов изображена оранжевыми и синими точками. Цель обучения нейронной сети понять, как описать класс новой точки зная её координаты (x1, x2). Выхоит что это простое задание не может быть решено с помощью однослойной архитектуры, так как оди слой может вмещать только рисование прямой линии во входяем пространестве (x1,x2). Давайте добавим еще одни слой.

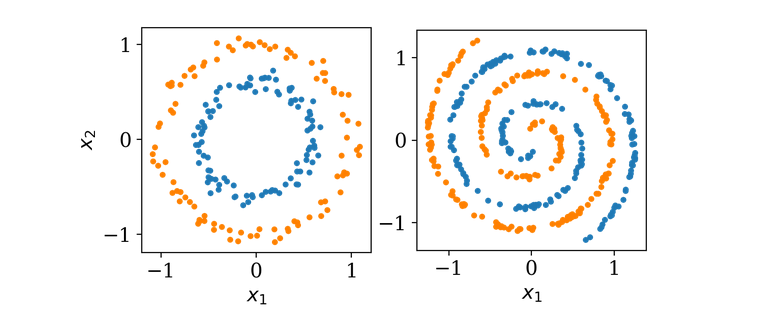
Двуслойная сеть.

Ввод x1 и x2 - меремножаются весами матрицы W1, затем функция активации f1 применяется поэлементно. Наконец, данные преобразуются с помощью W2 и затем следующей функцией активации f2(не отображена) чтобы получить вывод y.

Картинка выше показывает однослойный скрытый нейронную архитектуру, которую мы будем взаимозамеяемо вызывать двух уровневую сетку: где f1(x) = max(0,x) так же известно как выпрямитель, будет первой активационной функцией и сигмоид f2(x)=σ(x)=[1+e^-1]^-1 - будет второй активационной функцией, которую вы уже видели в прошлой статье. Специфика сигмоида приводить вохдные данные к виду от 0 до 1. Этот вывод имеет тендецию быть ползеным в нашем случае где мы только имеет два класса: синие точки обозначенные как 0 и оранжевые точки как 1. Для минимизации функции потери во время обучения нейронной сети, мы будем использовать функция доичной перекресной энтропии: 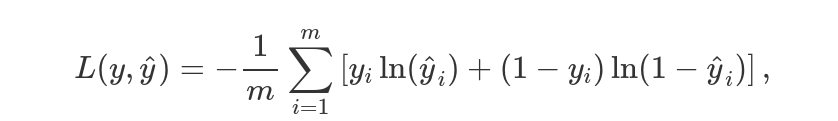где y желаемый вывод а ^y предсказание нейронной сети. Эта функция потери была специально создана что эффективного научения нейронной сети. Другое преимущество перекресной энтрпии в том, что в соединении с активацией сигмоида, градиент ошибки является просто разницей между предсказанным и желаемым выводом.

С каких значений начать?

Первая ошибка может закрастся в полное игнорирование важности первоначального задания весов сети. Естественно, вы хотите созать нейрон способный обучаться различным свойствам. Далее, вы хотите указать веса нейронной сети случайно. 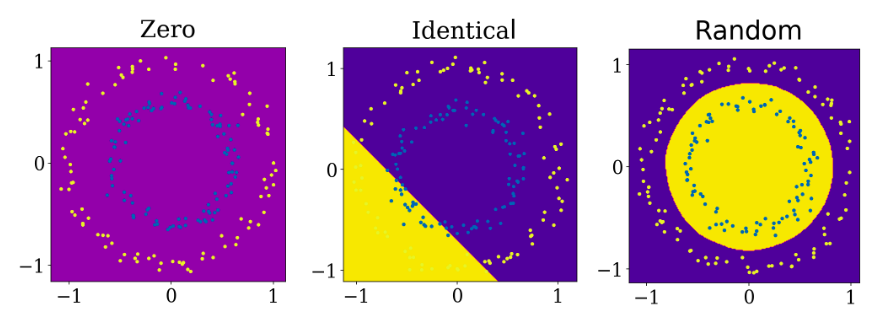Проблема круга. Решение о размере границ нейронной сети обучено с помощью метода градиентного спуска с заданными нулевыми весами(1), одинаковыми весами(2) и разными весами(3)

Выше мы можем увидеть разрешение границы для этих трех начальных случаем. Первое, когда веса заданы нулевыми, сеть не может чему-то научиться. Во втором случае, веса заданы не нулями а одинаковыми значениями, в этом случае нет ясности между отдельными нейронами. Далее, вся сеть становится одним большим нейроном. Наконец когда в нейронной сети заданы случайные числа, она может учиться.

Как обучать?

Универсальная теорема приближения говорит, что под конкретным предположением, однослойная скрытая архитектура должна быть достаточной для приближения любой ризонной функции. Однако, она ничего не говорит о том, как получить или насколько сложно получить веся для нейронной сети. Как мы видели на примере задания весов, использование простого обучения градиентного спуска для обучения, наша сеть смогла различить два круга. Теперь, что на счет более сложного примера: спираль, которая сложна в силу своей нелинейности. Посмотрим на анимацию ниже, слева, чтобы увидать как обучение простого градиентного спуска может легко застрять в неоптимальных настройках.

Проблемы спирали. Обе нейронные сети имеют однлослойную скрытую архитектуру с 512 нейронами. Левый обучен с помощью простого градиентного спуска, правый обучен спомощью Adam.

Сеть не может определится между классами. Кто-то может предположить что нужна более адекватная нейронная сеть. Что от части верно. Однако, упомянутая выше теорема подсказывает что это может быть не нужным.

Выходит, что много разработок нейронной сети и глубого обучения именно том, как настроить веса, это все что есть в неронном алгоритме. Недостаток прямого градиентного спуска, который алгоритр часто затыкается задолго до приемлимого решения. Одна из воможностей облегчить это ввести импельс. Возможно, самый популярный среди алгоритмов с импульсом - Adam. Как мы можем увидеть из картинки выше справа, алгоритм Adam может эффективно строить подходящие рамки решения. Мне кажется более показательным, если мы изобразим вывод нейронной сети во вмеря обучения.

Проблемы спирали. Вывод двух обучаемых моделение перед пороговым значением. Можно увидеть, что алгоритм GD частично застрял в промежуточном состоянии, где алгоритм Adam эффективно ведет к разделению двух классов.

Таким образом мы видим, что сходимость алгоритма Adam быстрее при более детальном рассмотрении. Если вы хотите изучить по подробнее раличные алгоритмы из семейства градиентного спуска, вот вам хорошее сравнение.

Как избежать ловушки линейного классификатора?

Теперь, что если мы по ошибке предоставили функцию линейной активации. Что случится? Если активация f будет линейной, тогда модел в формуле 2 урежится до однослойной нейроннйо сети.

где c - константа. W - линейный классификатор. Это может быть видно на результате границ решения.

Двуслойная сеть с активационной функцией f(x)=x.

Мы использовали ту же архитектуру что и выше, за исключением функции активации f(x)=x. Теперь мы видит, что двуслойная нейронная сеть действует как простая однослойная сеть: она может только делить входящее пространство используя прямые линии. Чтобы избежать этого, все функции активации должны оставаться нелинейными.

Сколько уровней?

Мы решили проблему спирали с помощью одного спрятанного уровня сети. Почему бы не добавить больше уровнеий? Чтобы задать этот вопрос, давайте нарисуем границы реления во время обучения нейронной сети для трех различных архитектур. Все нейронные сети имеют ReLU активацию вне терминальных уровней и сигмоид на последнем уровне. Как можно увидеть из кратинки ниже, сеть с тремя спрятанными уровнями и с несколькими нейронами в каждом уровне, обучается быстрее. Причина может быть ясна интуитивно. Нейронная сеть производит топологическое преобразование входного пространства. Составляя несколько простых преобразований ведущих к одному более сложному. Отсюда, для таких нелинейных разделенных классов, как в проблеме спиралей, имеем только преимущество от добавления уровней.

Неронная сеть обучает сходимост(Adam). Архитектуры:(1) один спрятанный уровень с 128 нейронами(513 параметров), (2) один спрятанный уровень с 512 нейронами(2049 параметров), (3) три спрятанных уровня с 40, 25 и 10 нейронами(1416 параметров). Наибольшую скорость схождения показывает последняя архитектура.

Из рисунка мы можем заключить, что больше нейроном не всегда лучший выбор. Самая яркая граница указывает на высшую уверенность в меньшем количестве шагов, полученных с помощью трех спрятанных уровней нейронной сети. Эта нейронная сеть имеет 1416 параметров считающих оба веса и отклонения. Это число около 30 процентов, меньше чем во второй архитектуре с одним одним спрятанным уровнем. Конечно, возможно нужно аккуратно выбирать архитектуру(три ссылки) рассматривая различные условия такие как размер набора данных, отклонение, входную размерность, тип задания и другое. С большим количеством уровней, нейронная сеть может более эффективно отражать сложные отношения. С другой стороны, если количество слоев очень большое, возможно придется применить различные приемы чтобы избежать такие проблемы как затухающий градиент.

Дана вся вводная информация, как на счет поэкспериментировать с нейронной сетью? В оставшейся части этой статьи мы научимся как строить многослойные нейронные сети на Haskell.

Реализация обратного распространения

В прошлой статье, мы реализовали обратное распространение для однослойной(без скрытого уровня) нейронной сети. Этот метод легко расширяется на пути движения к многослойное сетке. Есть пример хорошего видео, где можно найти много технических деталей. Ниже мы вспомним как обратное распространение работает для каждого нейрона.

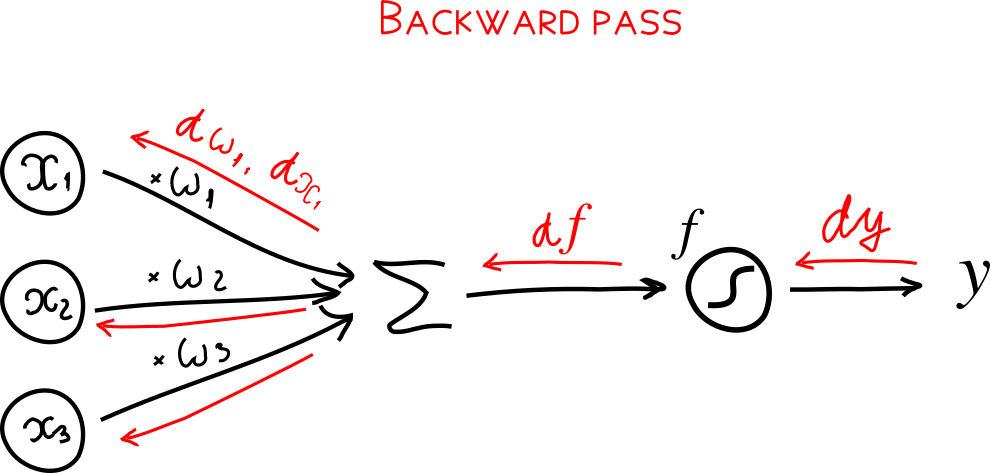
*Обратное распространение для нейрона. Вычисления нейрона известно как forward pass показано черным цветом. backward pass обратное распространение градиента в обратном направлении обозначено красным.

Если вы найдете любой другой пример обратного распространения, шансы что вы сначала реализуете так называемое forward pass и затем, как отдельную функцию backward pass. Проход вперед вычисляет вывод нейронной сети, где обратный обход ведет учет градиента. В прошый раз мы показали пример прохода вперед в однослоной архитектуре:

forward x w =
  let h = x LA.<> w
      y = sigmoid h
  in [h, y]

где h=x LA.<> w вычисляет ![] и y= sigmoid h это поэлементная активация 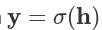. Здесь мы предоставили оба результата вычесления нейронной сети y и промежуточное значение h, которое было последовательно использовано в обратном проходе для вычисления весов градиента dW:

    dE = loss' y y_target
    dY = sigmoid' h dE
    dW = linear' x dY

Если есть несколько слоев, то два прохода(вперед и назад) обычно вычисляют все промежуточные результаты 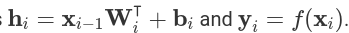Затем эти средние значения используются в обратном порядке для вычисления dW.