День 3: Haskell путеводитель по нейронным сетям

NowПосле thatтого weкак haveмы seenпосмотрели, howкак neuralработает networksсеть, work,стало weясно, realizeчто thatпонимание understandingградиента ofжизненно theнеобходимо. gradientsОтсюда, flowпересмотрим isнашу essentialстратегию forна survival.уровне Therefore,ниже. weОднако, willтак reviseкак ourнейронные strategyсети onстановятся theсложнее, lowestвычисления level.градиента However,в asручном neuralрежиме networksстановится becomeеще moreтем complicated,делом. calculationНо ofвсё gradientsеще byесть handвыход! becomesЯ aочень murkyрад, business.что Yet,сегодня fearмы notнаконец youngпознакомимся padawan,автоматической thereдифференциацией, isестественным aинструментом wayв out!изучении Iарсенала amглубокого veryобучнеия. excitedЭта thatстатья todayнаписана weпод willвпечатлением finally get acquainted with automatic differentiation, an essential tool in your deep learning arsenal. This post was largely inspired byот Hacker's guide to Neural Networks. ForДля comparison,сравнения seeтак alsoже стоит посмотреть Python version.версию.

Before

Почему jumpingслучайный ahead,локальный youпоиск mayне also want to check the previous posts:

• Day 1: Learning Neural Networks The Hard Way
• Day 2: What Do Hidden Layers Do? The source code from this guide is available on Github. The guide is written in literate Haskell, so it can be safely compiled.

Why Random Local Search Failsподходит

FollowingСледуя Karpathy'sинструкции guide,от weКартпатого, firstдля considerначала aрассмотрим simpleпростую multiplicationцепь circuit. Well,умножений. Haskell isне notJavascript, JavaScript,поэтому soперепишем theявным definition is pretty straightforward:образом.

forwardMultiplyGate = (*)

Or we could have written

forwardMultiplyGate x y = x * y

toчтобы makeсделать theфункцию functionболее look more intuitivelyпонятной f(x,y)=x⋅y. Anyway,В любом случае,

forwardMultiplyGate (-2) 3

returnsВозвращает -6. Exciting.Отлично!

Now,Теперь theвопрос: question:есть isли itвозможность possible to change the inputизменить (x,y) slightlyчтобы inулучшить orderвывод? toОдин increaseиз theспособов output?это Oneпроизвести wayлокальный wouldслучайный be to perform local random search.поиск.

_search tweakAmount (x, y, bestOut) = do
  x_try <- (x + ). (tweakAmount *) <$> randomDouble
  y_try <- (y + ). (tweakAmount *) <$> randomDouble
  let out = forwardMultiplyGate x_try y_try
  return $ if out > bestOut
               then (x_try, y_try, out)
               else (x, y, bestOut)

NotНе surprisingly,удивительно, theфункция functionвыше aboveотражает representsпростую aитерацию singleцикла iterationfor. ofЧто aон "for"-loop.делает: Whatслучайным itобразом does,выбирает itточки randomlyвокруг selects points around initialначальных (x,y) andи checksпроверяет ifувеличился theли outputвывод. hasЕсли increased.да, Ifтогда yes,он thenобновляет itлучшие updatesизвестные theвходные bestи knownмаксимальные inputsвыходные andданные. theЧтобы maximalпройтись output.по Toзначениям, iterate,мы weможем can useиспользовать foldM :: (b -> a -> IO b) -> b -> [a] -> IO b. ThisЭта functionфукнция isудобна convenientтак sinceкак weожидаем anticipateвзаимодействие some interaction with theс "externalреальным world"миром" inв theвиде formслучайно ofсгенерированных random numbers generation:чисел.

localSearch tweakAmount (x0, y0, out0) =
 foldM (searchStep tweakAmount) (x0, y0, out0) [1..100]

Код говорит нам, что мы наполняем код с какими-то начальными значениями x0, y0 и out0 и проходимся от 1 до 100. Ядро алгоритма - searchStep What the code essentially tells us is that we seed the algorithm with some initial values of x0, y0, and out0 and iterate from 1 till 100. The core of the algorithm is searchStep:

searchStep ta xyz _ = _search ta xyz

whichчто isесть aдовольно convenienceудобная functionфункция, thatкоторая gluesсклеивает those2 twoчасти piecesвместе. together.Она Itпросто simplyигнорирует ignoresитерационные theчисла iterationи numberвызывает and_search. callsТеперь, _search.нам Now,нужно weслучайное wouldчисло likeв to have a random number generator within the range ofпромежутке [-1; 1). FromИз theдокументации, documentation,мы weзнаем, know thatчто randomIO producesпроизводит aчисла number betweenмежду 0 andи 1. Therefore,Проскалируем weего scaleумножая the value by multiplying byна 2 andи subtractingвычитая 1:1.

randomDouble :: IO Double
randomDouble = subtract 1. (*2) <$> randomIO

TheФункция <$> functionэто is a synonym toсиноним fmap. WhatОна itприменяет essentiallyчистую does is attaching the pure functionфункцию subtractsubstract 1. (*2) whichтип has typeкоторой Double -> Double-Double, to theко "externalвнешнему" world" actionдействию randomIO, whichтип has typeкоторой IO Double (yes, IO = input/output)1.

AХитрость hackдля forчисла aминус numerical minus infinity:бесконечность:

inf_ = -1.0 / 0

Now,Теперь weзапускаем run localSearch 0.01 (-2, 3, inf_) severalнесколько times:раз:

(-1.7887454910045664,2.910160042416705,-5.205535653974539)
(-1.7912166830200635,2.89808308735154,-5.19109477484237)
(-1.8216809458018006,2.8372869694452523,-5.168631610010152)

InНа fact,деле weмы seeвидим thatкак theвывод outputsизменился have increased fromс -6 to aboutдо -5.2. ButНо theулучшение improvement is only about 0.8/100 =только 0.008 unitsедениц perна iteration.итерацию. ThatЭто isочень anне extremelyэффективный inefficientметод. method.Проблема Theсо problemслучайным withпоиском randomв searchтом, isчто thatкаждый eachраз timeон itпытается attemptsизменить toвходные changeданные theв inputsслучайных inнаправлениях. randomЕсли directions.алгоритм Ifделает theошибку, algorithmон makesдолжен aсбросить mistake,результат itи hasначать toс discardпоследней theлучшей resultпозиции. andНе startправда againли fromлучше theбыло previouslyбы, knownесли bestвместо position.каждой Wouldn'tитерации itрезультат beулучшался niceпусть ifдаже insteadпо eachчуть iterationчуть wouldно improveпостоянно theи resultне atприходилось least by a little bit?откатываться?

AutomaticАвтоматическое Differentiationдифференцирование

InsteadВместо ofслучайного randomпоиска searchв inслучайном randomнаправлении, direction,мы weможем canиспользовать makeточное useнаправление ofи theколичество preciseдля directionизменения andвходных amountданных toтаким changeобразом, theчтобы inputулучшался soвывод. thatИ theэто outputто wouldчто improve.градиент Andнам thatговорит. isВместо exactlyручного whatвычисления theградиента gradientкаждый tellsраз, us.мы Insteadможем ofиспользовать manuallyумный computingалгоритм. theЕсть gradientможноество everyподходов: time,цифровой, weсимволический canи employавтоматическое someдифференцирование. cleverВ algorithm.этой Thereстатье, existДоминик multipleСтейнтц approaches:объясняет numerical,разницу symbolic,между andними. automaticПоследений differentiation.подход, Inавтоматическое hisдифференцирование, article,именно Dominicто Steinitzчто explainsнам theнужно: differencesточные betweenградиенты them.с Theмнимальным lastколичеством approach,переработок. automaticКратко differentiationпоясним is exactly what we need: accurate gradients with minimal overhead. Here, we will briefly explain the concept.идею.

TheЗа ideaидеей behindавтоматического automaticдифференцирования differentiationстоит isясно thatопределенный weградиент explicitlyтолько defineдля gradientsпростых onlyбазовых forоператоров. elementary,Затем, basicмы operators.составляем Then,цепь weправил exploitкомбинируя theоператоры chainв ruleнейронную combiningсеть thoseкак operatorsхотим. intoТакая neuralстратегия networksбудет orвлиять whateverна weсам like.градиент. ThatДавайте strategyпосмотрим willна inferметод theчерез necessary gradients by itself. Let us illustrate the method with an example.пример.

BelowНиже weможно defineпосмотреть bothоператор multiplicationумножения operatorи andего itsградиент gradientиспользуя usingправило. the chain rule, i.e.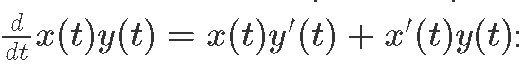

(x, x') *. (y, y') = (x * y, x * y' + x' * y)

TheТоже sameсамое canможно beсделать doneсо withсложением, addition,вычитанием, subtraction,делением division,и and exponent:экспонентой:

(x, x') +. (y, y') = (x + y, x' + y')

x -. y = x +. (negate1 y)

negate1 (x, x') = (negate x, negate x')

(x, x') /. (y, y') = (x / y, (y * x' - x * y') / y^2)

exp1 (x, x') = (exp x, x' * exp x)

WeМы alsoтак haveже имеем constOp forдля constants:констант:

constOp :: Double -> (Double,Double)
constOp x = (x, 0.0)

Finally,Наконец, weмы canможем defineопределить ourнаш favouriteлюбимый sigmoidсигмоид σ(x) combiningобъединяя theте operatorsоператоры, above:что были выше:

sigmoid1 x = constOp 1 /. (constOp 1 +. exp1 (negate1 x))

Now,теперь letдавайте usпосчитаем computeнейрон a neuron f(x,y)=σ(ax+by+c), whereгде x andи y areэто inputsввод andа a,a, b,b andи c are parametersпаарметры.

neuron1 [a, b, c, x, y] = sigmoid1 ((a *. x) +. (b *. y) +. c)

Now,Теперь weможно canполучить obtainградиент theдля gradienta ofв aточке in the point where (a=1, b=2, c=−3, x=−1, and y=3:3)

abcxy1 :: [(Double, Double)]
abcxy1 = [(1, 1), (2, 0), (-3, 0), (-1, 0), (3, 0)]

neuron1 abcxy1
(0.8807970779778823,-0.1049935854035065)

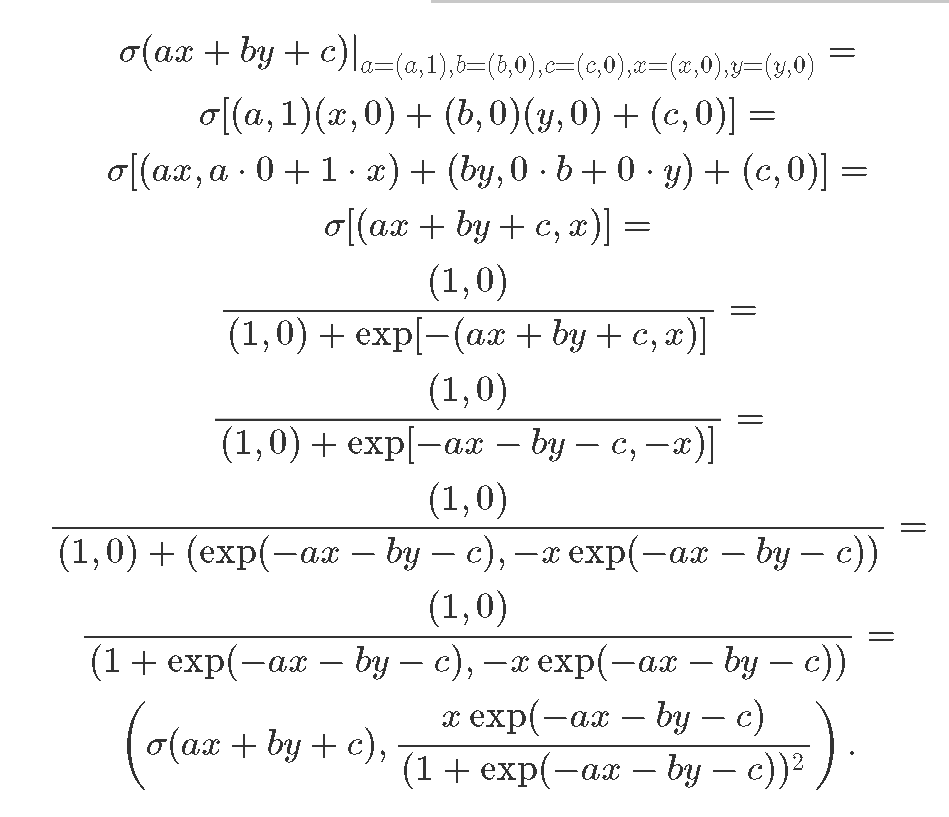
Here,Вотт theпервый firstпример numberрезультата isвывода theнейронно resultйсети ofи theвторой neuron'sградиент output and the second one is the gradient with respect toотносительно a LetПроверим usматематику verify the math behind the result:результата: TheПервое firstвыражение expressionэто isрезультат theвычислений resultнейронов, ofа neuron'sвторой computationточное andаналитическое theвыражение secondВот oneи isвся theмагия exactза analyticсловами expressionавтоматическая for

дифференциация. ThatПохожим isобразом, allмы theможем magicполучить behindостаток automatic differentiation! In a similar way, we can obtain the rest of the gradients:градиента: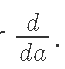

neuron1 [(1, 0), (2, 1), (-3, 0), (-1, 0), (3, 0)]
(0.8807970779778823,0.3149807562105195)

neuron1 [(1, 0), (2, 0), (-3, 1), (-1, 0), (3, 0)]
(0.8807970779778823,0.1049935854035065)

neuron1 [(1, 0), (2, 0), (-3, 0), (-1, 1), (3, 0)]
(0.8807970779778823,0.1049935854035065)

neuron1 [(1, 0), (2, 0), (-3, 0), (-1, 0), (3, 1)]
(0.8807970779778823,0.209987170807013)

IntroducingВведение backpropбиблиотеки libraryобратного распределения

TheБиблиотека backpropобратного libraryраспределения wasбыла specificallyнаписана designedспециально forдля differentiableдифференциального programming.программирования. ItОна providesпредоставляет combinatorsкомбинаторов toдля reduceуменьшения ourнашей mentalголовной overhead.боли. InВ addition,добавок, theсамые mostполезные usefulоперации operationsарфиметические suchи asтригонометрические, arithmeticsуже andбыли trigonometry,определены haveв alreadyбиблиотеке. beenМожно definedвзглянуть inна the library. See also hmatrix-backprop forдля linearлинейной algebra.алгебры. SoВсё allчто youвам needнужно forдля differentiableдифференциального programmingпрограммирования nowопределить isнесколько to define some functions:функций:

neuron
  :: Reifies s W
  => [BVar s Double] -> BVar s Double
neuron [a, b, c, x, y] = sigmoid (a * x + b * y + c)

sigmoid x = 1 / (1 + exp (-x))

HereТут BVar sобернут wrapperв signifiesмаркер thatтого, ourчто functionфункция is differentiable. Now, the forward pass is:дифференцируемая.

forwardNeuron = BP.evalBP (neuron. BP.sequenceVar)

WeИспользуем useизоморфимз sequenceVar isomorphismдля to convert aпреобразования BVar ofсписок aв list into a list ofсписок BVars,ов, asкак requiredтого byтребует ourвыражение neuron. equation.И Andпередаем the backward pass isдальше.

backwardNeuron = BP.gradBP (neuron. BP.sequenceVar)

abcxy0 :: [Double]
abcxy0 = [1, 2, (-3), (-1), 3]

forwardNeuron abcxy0
-- 0.8807970779778823

backwardNeuron abcxy0
-- [-0.1049935854035065,0.3149807562105195,0.1049935854035065,0.1049935854035065,0.209987170807013]

NoteЗаметим, thatчто allвсе theградиенты gradientsв areодном inсписке, oneтип list,аргумента theпервого type of the first neuron argument.нейрона.

SummaryВыводы

ModernСовременная neuralнейронная networksсеть tendтяготеет toк beсложности. complexНаписание beasts.градент Writingобратного backpropagationраспределения gradientsв byручну handможет canлегко easilyстать becomeужасом. aВ tediousэтом task.посте Inмы thisпосмотрели postкак weможно haveавтоматизировать seenэтот howпроцесс automaticпри differentiation can face this problem.надобности.

InВ theследующем nextпосту postsмы weприменим willавтоматическую applyдифференциацию automaticк differentiationреальной toсетке. realПоговорим neuralо networks.нормализации, Weдругих willважных talkметодахв aboutглубоком batchобучении. normalization,И anotherзатронем crucialсверточные methodнейнонные inсети, modernкотороые deepпомогут learning.нам Andрешить weинтересные will ramp it up to convolutional networks allowing us to solve some interesting challenges. Stay tuned!задачи.

FurtherЧто readingможно почитать.

Visual guide to neural networks Backprop documentation Article on backpropagation by Dominic Steinitz