День 2: Что делают скрытые уровни?

На прошлом дне, мы ввели понятие обучения одноуровней нейронной сети. Сегодня мы узнаем преимущества многослойной нейронной сети, как правильно её организовывать и обучать.

Когда я обсуждаю нейронную сетку со студентами, которые только начали открывать технику машшиног обучения:

-Я сделал сетку распознавания цифр рукописного ввода. Но моя точность всего лишь Y

-Кажется это горазно меньше чем последнее слово техники, - размышляю я.

-Вот именно. Может быть прроблема в X?

Обычно X это не причина. Реальная причина должна быть более простая: вместо многослойной нейронной сети студент сделал однослойную нейронную сетку или её эквивалент. Эта сеть работает как линейный классификатор, следовательно она не может выучить не ленейные отношения между входом и желаемым выводом.

Так что такое многослойная нейронная сеть и как избежать ловушки с линейной классификацией.

Многослойная нейронная сеть.

Многослойная нейронная сеть, может быть описана как: где x и y это входные и выходные векторы соответственно, - веса матриц и смещение векторов, и 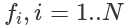функции активации в i'том слое. Нелинейная функция активации f применяется поэлемментно.

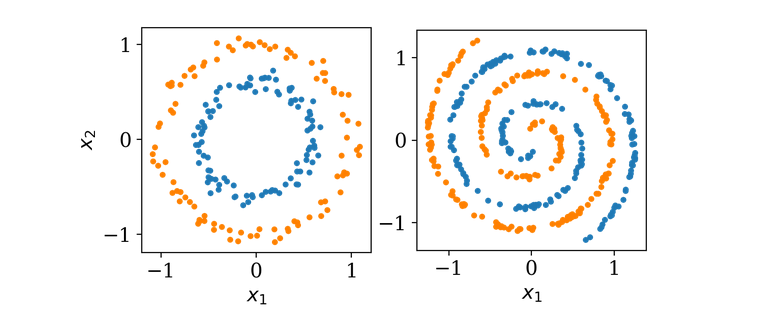
В качестве примера мы сегодня будем использовать двумерный набор данных как показано ниже.

Оба набора свойств двху классов изображена оранжевыми и синими точками. Цель обучения нейронной сети понять, как описать класс новой точки зная её координаты (x1, x2). Выхоит что это простое задание не может быть решено с помощью однослойной архитектуры, так как оди слой может вмещать только рисование прямой линии во входяем пространестве (x1,x2). Давайте добавим еще одни слой.

Двуслойная сеть.

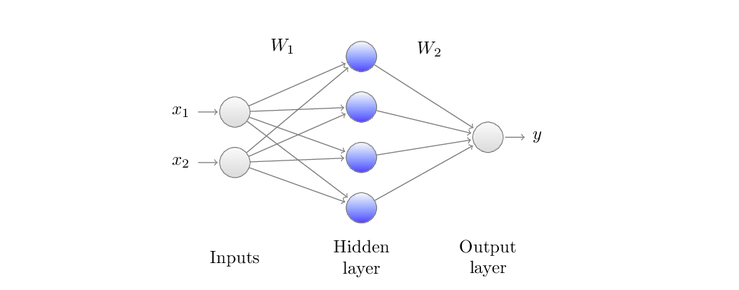
Ввод x1 и x2 - меремножаются весами матрицы W1, затем функция активации f1 применяется поэлементно. Наконец, данные преобразуются с помощью W2 и затем следующей функцией активации f2(не отображена) чтобы получить вывод y.

Картинка выше показывает однослойный скрытый нейронную архитектуру, которую мы будем взаимозамеяемо вызывать двух уровневую сетку: где f1(x) = max(0,x) так же известно как выпрямитель, будет первой активационной функцией и сигмоид f2(x)=σ(x)=[1+e^-1]^-1 - будет второй активационной функцией, которую вы уже видели в прошлой статье. Специфика сигмоида приводить вохдные данные к виду от 0 до 1. Этот вывод имеет тендецию быть ползеным в нашем случае где мы только имеет два класса: синие точки обозначенные как 0 и оранжевые точки как 1. Для минимизации функции потери во время обучения нейронной сети, мы будем использовать функция доичной перекресной энтропии: 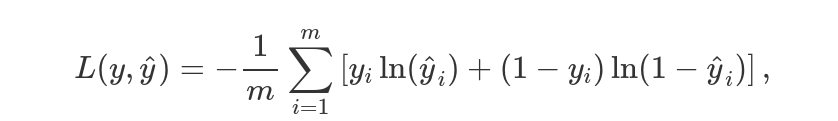где y желаемый вывод а ^y предсказание нейронной сети. Эта функция потери была специально создана что эффективного научения нейронной сети. Другое преимущество перекресной энтрпии в том, что в соединении с активацией сигмоида, градиент ошибки является просто разницей между предсказанным и желаемым выводом.

С каких значений начать?

Первая ошибка может закрастся в полное игнорирование важности первоначального задания весов сети. Естественно, вы хотите созать нейрон способный обучаться различным свойствам. Далее, вы хотите указать веса нейронной сети случайно. 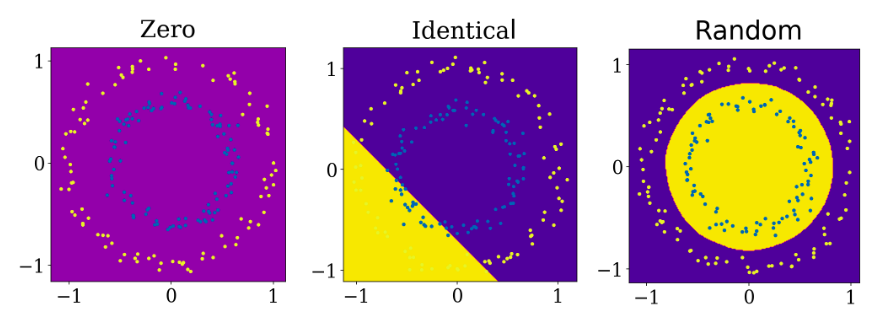Проблема круга. Решение о размере границ нейронной сети обучено с помощью метода градиентного спуска с заданными нулевыми весами(1), одинаковыми весами(2) и разными весами(3)

Выше мы можем увидеть разрешение границы для этих трех начальных случаем. Первое, когда веса заданы нулевыми, сеть не может чему-то научиться. Во втором случае, веса заданы не нулями а одинаковыми значениями, в этом случае нет ясности между отдельными нейронами. Далее, вся сеть становится одним большим нейроном. Наконец когда в нейронной сети заданы случайные числа, она может учиться.

Как обучать?

Универсальная теорема приближения говорит, что под конкретным предположением, однослойная скрытая архитектура должна быть достаточной для приближения любой ризонной функции. Однако, она ничего не говорит о том, как получить или насколько сложно получить веся для нейронной сети. Как мы видели на примере задания весов, использование простого обучения градиентного спуска для обучения, наша сеть смогла различить два круга. Теперь, что на счет более сложного примера: спираль, которая сложна в силу своей нелинейности. Посмотрим на анимацию ниже, слева, чтобы увидать как обучение простого градиентного спуска может легко застрять в неоптимальных настройках. Проблемы спирали. Обе нейронные сети имеют однлослойную скрытую архитектуру с 512 нейронами. Левый обучен с помощью простого градиентного спуска, правый обучен спомощью Adam.