День 4: Важность пакетной нормализации

Для какой цели существуют нейронные сети? Нейронные сети - это обучаемые модели. Их главная цель - приблизиться или даже превзойти человеческие способности восприятия. Ричард Суттон говорит, что самый большой уро, который может быть получен с 70 годов разработки ИИ, в том, что общие методы использующие вычисления очень эффективны. В его эссе, Суттон говорит, что только модели без зашифрованного человеческого знания могут превзойти человеко-ориентированные подходы. Так, что нейронные сети в общем будут достаточны для использования вычислений. Затем, не удивительно, что они могут выставить миллионы обучаемых степеней свободы.

Самый большой вызов для нейронных сетей: 1) как обучить эти миллионы параметров, 2) как их интерпритировать. Пакетная нормализация(batchnorm) был представлен в качестве попытки сделать обучение еще эффективнее. Метод может сильно сократить число итераций обучения. Даже больше, batchnorm - возможо является ключем, который даст возможность обучать определенные архитектуры такие как бинарная нейронная сеть. Наконец, batchnorm одна из самых последних преимуществ нейронной сети.

Пакетная нормализация в кратце

Что такие пакет? До сих пор, вы смотрели на игрущечные наборы данных. Они были настолько малы, что могли быть легко помещены в память. Однако, в реальности существует огромные наборы занимающие сотни гигабайтов памяти, такие как Imagenet. Они часто не помещаются в память. В этом случае, имеет смысл разделить наборы данных в маленькие пакеты. Во время обучения обрабатывается только один пакет.

Как предполагает имя, batchnorm преобразование это действие над отдельными пакетами данных. Вывод линейного слоя может быть причиной деградации активационной функции. Например: в случае ReLU f(x)=max(0,x) активация, все негативные значения будут приводить к нулевой активации. Отсюда, хорошая идея - нормализовать эти значения с помощью вычитания среднего μ пакета. Похожим образом, деление по стандартному отклоненю √var масштабирует амплитуту, которая особенно выгодня для активация сигмоидного вида.

Обучение и Batchnorm

Процеедура пакетной нормализации имеет отличия на этапах обучения и вывода. Во время обучения, каждый слой, где мы хотим применить batchnorm, сначала вычисляем средний мини пакет:

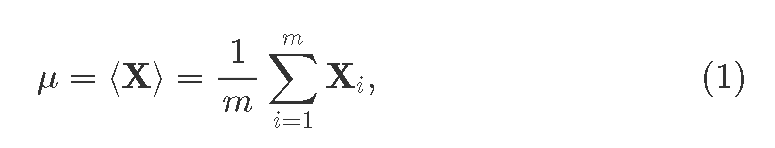где Xi это i вектор-свойство идущий из прошлого слоя; i=1…m, где m>1 это размер пакета. Так же получаем ди:сперсию для пакета

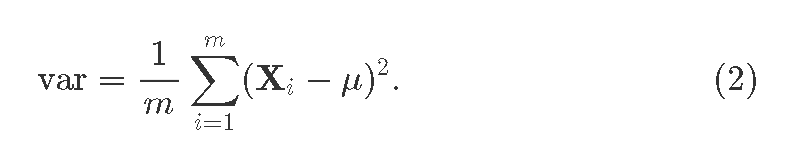
Теперь batchnorm ядро, сама нормализация: где маленькая постоянная ϵ добавляет числовую стабильность. Что если нормализация данного слоя была вредна? Алгоритм предоставит два обучаемых параметра, которые в худшем случае могут отменить эффект пакетной нормализации: смасштабирует параметр γ и увеличит β. После применения таковых мы получим вывод слоя batchnorm: Отметим, что оба: среднее значениее μ и распределение var векторы количество которых такое же большое как и нейронов в данном скрытом слое. Оператор ∗ говорит о поэлементном умножении.

Вывод

В стадии вывода лучше всего иметь одну выборку данных за раз. Как же сосчитать среднюю величину пакета если целый пакет это и есть выборка данных? Для правильной обраотки, во время обучения мы указываем среднее значение и распределение (E[X] and Var[X]) для всех наборов обучения. Эти вектора заменят μиvar` во время вывода, таким образом избегая проблемы нормализации единичного пакета.

Насколько эффективен Batchnorm

До этого момента мы успели поиграться с задачами, которые предоставляют свойство низкоразмерного ввода. Теперь, мы собираемся протестировать нейронную сеть проблемой по серьезнее. Мы применим наши навыки для автоматического распознавания написанных человеком цифр на основе известного MNIST набора данных. Эта проблем появляется в следствии нужды чтения кодов с конветов на почте.

Мы создадим две нейронные сети, каждая бдует иметь два полностью связанных скрытых слоя (300 и 50 нейронов). Обе сети получают картинку размером 28×28=784 пикселей, и возвращает 10 чисел, распознанное число. Для внутненних слоев мы будем использовать ReLU f(x)=max(0,x). Для получения возможных классификаторов вектора в результате, в качестве функции активации мы будем использовать . Одна из сетей в дополнение будет производить пакетную нормализацию перед ReLU. Затем, мы будем обучать их использую стохастический градиентный спуск с коэфиициентом обучения α=0.01^3 и размером пакета m=100.

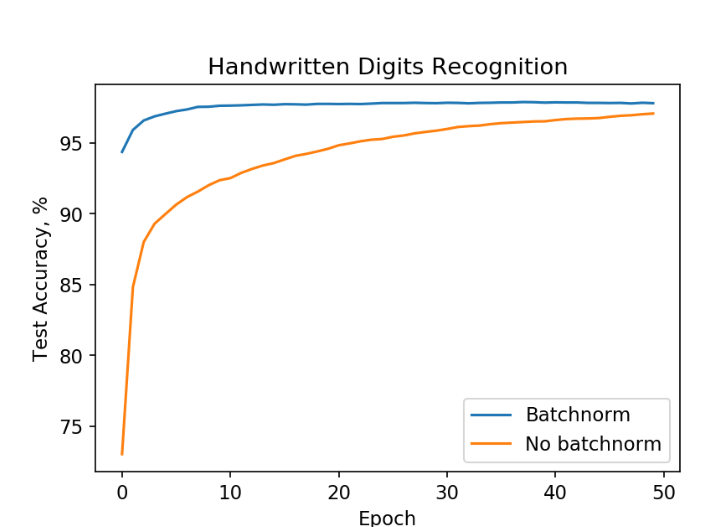
Обучение нейронной сети на MNIST данных.

Обучение с помощью пакетной нормализации (синий график) ведет к высокой точности быстрее чем без нее(ораньжевый график).

Из графика мы видим, что нейронная сеть с пакетной нормализацией достикает точности в 98% за 10 эпох, где второй пыатеся сделать это в течении 50!Похожие результаты могут быть получены другими архитектурами.

Надо упомянуть, что мы до сих пор может слабо недостаточно понимать как именно batchnorm помогает. В его оригинальном описание, предполагается, что batchnorm сокращает внутренее ковариантное смещение. Недавно, было показано, что это не обязательно правда. Лучшее на сегодняшний день объяснение то, что batchnorm делает оптимизационные сглаживания, которые делают обучение градиентным спуском эффективнее. Что, в свою очередь, позволяет ускорить процесс обучение с помощью batchnorm!

Реализация batchnorm

Мы воспользуемся кодом приведенным в дне 2. Первое, мы переопределим структура дынных Layer сделав его более детализированным:

data Layer a = -- Linear layer with weights and biases
               Linear (Matrix a) (Vector a)
               -- Same as Linear, but without biases
               | Linear' (Matrix a)
               -- Batchnorm with running mean, variance, and two
               -- learnable affine parameters
               | Batchnorm1d (Vector a) (Vector a) (Vector a) (Vector a)
               -- Usually non-linear element-wise activation
               | Activation FActivation

Превосходно! Теперь мы можем отделить несколько типов слоев: родственный(линейный), активационный и batchnorm. Так как batchnorm уже компенсирует смещения, нам не нужно использовать смещения на последующих слоях. Поэтому мы определяем Linear слой без смещений. Так же расширим Gradients для использования новой структуры слоёв:

data Gradients a = -- Weight and bias gradients
                   LinearGradients (Matrix a) (Vector a)
                   -- Weight gradients
                   | Linear'Gradients (Matrix a)
                   -- Batchnorm parameters and gradients
                   | BN1 (Vector a) (Vector a) (Vector a) (Vector a)
                   -- No learnable parameters
                   | NoGrad

Теперь, мы хотим расширить функцию распространения нейронной сети _pass, в зависимости от слоя. Это проще всего сделать с помощью с сопоставления с образцом. Вот как мы это сделаем в Batchnorm1d слое и его параметрах:

    _pass inp (Batchnorm1d mu variance gamma beta:layers)
        = (dX, pred, BN1 batchMu batchVariance dGamma dBeta:t)
      where

Как и раньше, _pass функция получает ввод inp и параметры слоя. Второй аргумент это образец с который мы и проводим сопоставление, создавая наш алгоритм, в данном случае, Batchnorm1D. Мы также указываем _pass для других видово слоев. Отсуда, мы получаем полиморфную функцию _pass для каждого слоя. Наконец, результат выражения является кортеж: градиенты для обратного распространения dX, предсказание pred и дополнительные данные t с вычисленными значениями BN1 в этом слое(средний пакет batchMu, распределение batchVariance и параметры градиентов для обучения).

Следующий шаг показан ниже:

        -- Forward
        eps = 1e-12
        b = br (rows inp)  -- Broadcast (replicate) rows from 1 to batch size
        m = recip $ (fromIntegral $ rows inp)

        -- Step 1: mean from Equation (1)
        batchMu :: Vector Float
        batchMu = compute $ m `_scale` (_sumRows inp)

        -- Step 2: mean subtraction
        xmu :: Matrix Float
        xmu = compute $ inp .- b batchMu

        -- Step 3
        sq = compute $ xmu .^ 2

        -- Step 4: variance, Equation (2)
        batchVariance :: Vector Float
        batchVariance = compute $ m `_scale` (_sumRows sq)

        -- Step 5
        sqrtvar = sqrtA $ batchVariance `addC` eps

        -- Step 6
        ivar = compute $ A.map recip sqrtvar

        -- Step 7: normalize, Equation (3)
        xhat = xmu .* b ivar

        -- Step 8: rescale
        gammax = b gamma .* xhat

        -- Step 9: translate, Equation (4)
        out0 :: Matrix Float
        out0 = compute $ gammax .+ b beta

Обсуждая в статье "День 2", мы повторяли вызов получения градиентов следующего слоя, нейронная сеть предсказывала pred и вычисляла значение хвоста t:

        (dZ, pred, t) = _pass out layers

Я предпочитаю хранить обратную передачу без упрощений. Это помогает прояснить какой из шагов за что отвечает:

        -- Backward

        -- Step 9
        dBeta = compute $ _sumRows dZ

        -- Step 8
        dGamma = compute $ _sumRows (compute $ dZ .* xhat)
        dxhat :: Matrix Float
        dxhat = compute $ dZ .* b gamma

        -- Step 7
        divar = _sumRows $ compute $ dxhat .* xmu
        dxmu1 = dxhat .* b ivar

        -- Step 6
        dsqrtvar = (A.map (negate. recip) (sqrtvar .^ 2)) .* divar

        -- Step 5
        dvar = 0.5 `_scale` ivar .* dsqrtvar

        -- Step 4
        dsq = compute $ m `_scale` dvar

        -- Step 3
        dxmu2 = 2 `_scale` xmu .* b dsq

        -- Step 2
        dx1 = compute $ dxmu1 .+ dxmu2
        dmu = A.map negate $ _sumRows dx1

        -- Step 1
        dx2 = b $ compute (m `_scale` dmu)

        dX = compute $ dx1 .+ dx2

Часто, нам нужно произвести операции типа вычитания среднего X−μ, где, на практике, у нас есть матрица X и вектор μ. Как вычесть вектор из матрицы? Правильно, никак. Вычитать можно только 2 матрицы. Такие библиотеки как Numpy могут говорить о магии, которая упростит превращение вектора в матрицу. Это может быть полезно, но может выявить различные виды багов. Мы же взамен произведем явное преобразование вектора в матрицу. Для наших нужд, мы имеем скращение b = br (rows inp), которое мы расширим вектор на то же число рядов как в inp. Где функция br ('broadcast'):

br rows' v = expandWithin Dim2 rows' const v

Это пример того, ка кработае br. Для начала, интерактивно запустим сессию и загрузим модуль NeuralNetwork.hs:

$ stack exec ghci
GHCi, version 8.2.2: http://www.haskell.org/ghc/  :? for help
Prelude> :l src/NeuralNetwork.hs

Затем проверим br функцию на векторе [1, 2, 3, 4]:

*NeuralNetwork> let a = A.fromList Par [1,2,3,4] :: Vector Float
*NeuralNetwork> a
Array U Par (Sz1 4)
  [ 1.0, 2.0, 3.0, 4.0 ]

*NeuralNetwork> let b = br 3 a
*NeuralNetwork> b
Array D Seq (Sz (3 :. 4))
  [ [ 1.0, 2.0, 3.0, 4.0 ]
  , [ 1.0, 2.0, 3.0, 4.0 ]
  , [ 1.0, 2.0, 3.0, 4.0 ]
  ]

Как можно увидеть, была получения новая матрица с тремя идентичными строками. Отметим, что As we can see, a new matrix with three identical rows has been obtained. Note that a hasимеет typeтип Array U Seq, meaningчто thatзначит, dataчто areданные storedхранятся inпростым anраспакованным unboxedмасивом.Где array.результат Whereas the result is of typeтипа Array D Seq так называемый отложенный массив. Этот отложенный массив, aна so-calledсамом delayedделе array.не Thisмассив, delayedно arrayтак isпонятнее notстановится, anчто actualэто array,будет butмассивом ratherв aдальнейшейм. promiseЧтобы toразместить compute6массив anв arrayпамяти in the future. In order to obtain an actual array residing in memory, useиспользуйте compute:

*NeuralNetwork> compute b :: Matrix Float
Array U Seq (Sz (3 :. 4))
  [ [ 1.0, 2.0, 3.0, 4.0 ]
  , [ 1.0, 2.0, 3.0, 4.0 ]
  , [ 1.0, 2.0, 3.0, 4.0 ]
  ]

YouПодробную willинформацию findможно moreполучить informationиз aboutбольшой manipulatingдокументации. arraysТак inже massivкак documentation.и Similarlybr, toсуществует br,несколько thereболее existудобных several more convenience functions,функций, rowsLike andи colsLike. ThoseОни areполезны usefulв inсвязке conjunction withс _sumRows andи _sumCols:

-- | Sum values in each column and produce a delayed 1D Array
_sumRows :: Matrix Float -> Array D Ix1 Float
_sumRows = A.foldlWithin Dim2 (+) 0.0

-- | Sum values in each row and produce a delayed 1D Array
_sumCols :: Matrix Float -> Array D Ix1 Float
_sumCols = A.foldlWithin Dim1 (+) 0.0

HereПример is an example ofиспользования _sumCols andи colsLike whenпри computingвычислении softmax activationактивационной функции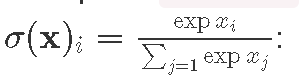

softmax :: Matrix Float -> Matrix Float
softmax x =
  let x0 = compute $ expA x :: Matrix Float
      x1 = compute $ (_sumCols x0) :: Vector Float
      x2 = x1 `colsLike` x
  in (compute $ x0 ./ x2)

NoteЗаметьте, thatчто softmax isотличается differentот fromпоэлементной element-wiseактивации. activations.Взамен, Instead,softmax softmaxдействует actsкак asполностью aсвязанный fully-connectedслой, layerкоторый thatполучает receivesи aотдает vectorвектор. andНаконец, outputsмы aопределяем vector.нашу Finally,нейронную weсеть, defineс ourдвумя neuralскрытыми networkслоями withи twoпакетной hiddenнормализацией linear layers and batch normalization as:так:

  let net = [ Linear' w1
            , Batchnorm1d (zeros h1) (ones h1) (ones h1) (zeros h1)
            , Activation Relu
            , Linear' w2
            , Batchnorm1d (zeros h2) (ones h2) (ones h2) (zeros h2)
            , Activation Relu
            , Linear' w3
            ]
```haskell

The

Число numberвходов ofэто inputsпроизведение is the total number of `28×28=784`784 imageпикселей pixelsкартинки andи theа numberвыход ofэто outputsчисло isклассов the number of classes (ten digits)т.е. Weцифр. randomlyМы generateслучайным theобразом initialсгенерировали weightsначальные `w1`веса w1, `w2`w2, and `w3`w3. AndИ setуказали initialначальный batchnormсостояние layerслоя parametersпакетной asнормализации follows:следующим meansобразом: toсреднее zeroes,число variances- to0, ones,распределение scaling- parameters1, toпараметры ones,масштабирования and- translation1, parametersи toсмещение zeroes:параметров ```haskell- 0:

  let [i, h1, h2, o] = [784, 300, 50, 10]
  (w1, b1) <- genWeights (i, h1)
  let ones n = A.replicate Par (Sz1 n) 1 :: Vector Float
      zeros n = A.replicate Par (Sz1 n) 0 :: Vector Float
  (w2, b2) <- genWeights (h1, h2)
  (w3, b3) <- genWeights (h2, o)

RememberПомним, thatчто theчисло numberпакетной ofнормализации batchnormдолжно parametersбыть equalsравно toчислу theнейронов. numberЭто ofраспространенная neurons.практика Itставить isпакетную aнормализацию commonперед practiceфункцие toактивации, putоднако batchэта normalizationпоследовательность beforeне activations,обязательна, howeverможно thisи sequenceна isоборот. notДля strict:сравнения, oneмы canсоставим putнейронную batchсеть normalizationс afterдвумя activationsспрятанными too.слоями Forбез comparison,пакетной we also specify a neural network with two hidden layers without batch normalization.нормализации.

  let net2 = [ Linear w1 b1
             , Activation Relu
             , Linear w2 b2
             , Activation Relu
             , Linear w3 b3
             ]

InВ bothобоих casesслучаях theвыход outputактивационной softmax activationизбегается isтак omittedкак asвычисляются itсовместно isс computedградиентами togetherпотерь withв lossконечном gradientsрекурсивном in the final recursive call inвызове _pass:

    _pass inp [] = (loss', pred, [])
      where
        pred = softmax inp
        loss' = compute $ pred .- tgt

Here,Здесь [] onс theлевой left-handстороны sideзначения signifiesэто anпустой emptyсписок listвходных ofслоёв, input layers, andа [] onс theправой right-handстороны sideэто isпустой theконец emptyвычисленных tailзначений ofв computedначале valuesобратного in the beginning of the backward pass.

The complete project is available on Github. I recommend playing with different neuron networks architectures and parameters. Have fun!прохода.

BatchnormПодводные Pitfallsкамни пакетной нормализации

ThereЕсть areнесколько severalпотенциальных potentialловушек trapsпри whenиспользовании usingпакетной batchnorm.нормализации.

First,

batchnorm
• Пакетная isнормализация differentотличается duringво trainingвремя andобучения duringи inference.взаимодействия. ThatЧто makesделает yourвашу implementationреализацию moreболее complicated.сложной.
Second,
• Пакетная batchnormнормализация mayможет failне whenполучиться trainingпри dataобучении comeданных fromкоторые differentидут datasets.из Toразных avoidнаборов. theЧтобы secondизбежать pitfall,этого, itнужно isпросто essentialубедиться, toчто ensureлюбой thatпакет everyотражает batchцелый representsнабор theданных. wholeТо dataset,есть i.e.все itпакеты hasимеют dataодинаковую comingформу.
from

the

Выводы

same

Не distributionсмотря asна theподводные machineкамни, learningпакетная taskнормализация youважная areидея tryingи toостается solve.популярным Readметодом moreв aboutконтексте that.глубого обучения. Сила пакетной нормализации в том, что она может существенно сократить число обучаемых эпох или даже помочь достичь лучше точности нейронной сети. После этого обсуждения, мы готовимся приступь к понятиям сверточные нейронные сети и обучение с подкреплением. Оставайтесь на связи.

Summary

Что

Despite its pitfalls, batchnorm is an important concept and remains a popular method in the context of deep neural networks. Batchnorm's power is that it can substantially reduce the number of training epochs or even help achieving better neural network accuracy. After discussing this, we are prepared for such hot subjects as convolutional neural networks and reinforcement learning. Stay tuned!

AI And Neural Networksпочитать.

• Richard Sutton. The Bitter Lesson
• Using neural nets to recognize handwritten digits
• Batch normalization paper
• How Does Batch Normalization Help Optimization?
• On The Perils of Batch Norm

Haskell

• Why I think Haskell is the best general purpose language
• An opinionated beginner's guide to Haskell in mid 2019
• Massiv Array Library
• Alexey's presentation about massiv