День 4: Важность пакетной нормализации

Для какой цели существуют нейронные сети? Нейронные сети - это обучаемые модели. Их главная цель - приблизиться или даже превзойти человеческие способности восприятия. Ричард Суттон говорит, что самый большой уро, который может быть получен с 70 годов разработки ИИ, в том, что общие методы использующие вычисления очень эффективны. В его эссе, Суттон говорит, что только модели без зашифрованного человеческого знания могут превзойти человеко-ориентированные подходы. Так, что нейронные сети в общем будут достаточны для использования вычислений. Затем, не удивительно, что они могут выставить миллионы обучаемых степеней свободы.

Самый большой вызов для нейронных сетей: 1) как обучить эти миллионы параметров, 2) как их интерпритировать. Пакетная нормализация(batchnorm) был представлен в качестве попытки сделать обучение еще эффективнее. Метод может сильно сократить число итераций обучения. Даже больше, batchnorm - возможо является ключем, который даст возможность обучать определенные архитектуры такие как бинарная нейронная сеть. Наконец, batchnorm одна из самых последних преимуществ нейронной сети.

Пакетная нормализация в кратце

Что такие пакет? До сих пор, вы смотрели на игрущечные наборы данных. Они были настолько малы, что могли быть легко помещены в память. Однако, в реальности существует огромные наборы занимающие сотни гигабайтов памяти, такие как Imagenet. Они часто не помещаются в память. В этом случае, имеет смысл разделить наборы данных в маленькие пакеты. Во время обучения обрабатывается только один пакет.

Как предполагает имя, batchnorm преобразование это действие над отдельными пакетами данных. Вывод линейного слоя может быть причиной деградации активационной функции. Например: в случае ReLU f(x)=max(0,x) активация, все негативные значения будут приводить к нулевой активации. Отсюда, хорошая идея - нормализовать эти значения с помощью вычитания среднего μ пакета. Похожим образом, деление по стандартному отклоненю √var масштабирует амплитуту, которая особенно выгодня для активация сигмоидного вида.

Обучение и Batchnorm

Процеедура пакетной нормализации имеет отличия на этапах обучения и вывода. Во время обучения, каждый слой, где мы хотим применить batchnorm, сначала вычисляем средний мини пакет:

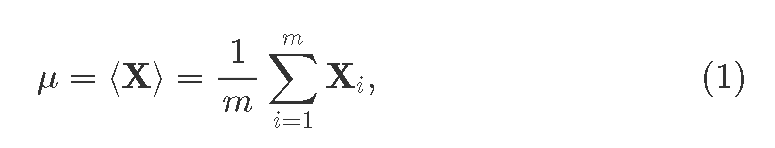где Xi это i вектор-свойство идущий из прошлого слоя; i=1…m, где m>1 это размер пакета. Так же получаем ди:сперсию для пакета

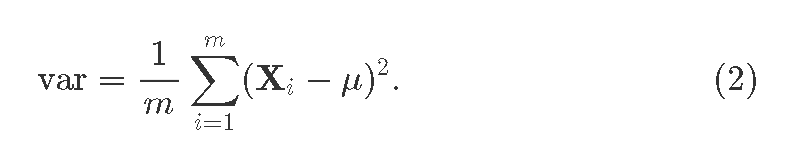
Теперь batchnorm ядро, сама нормализация: где маленькая постоянная ϵ добавляет числовую стабильность. Что если нормализация данного слоя была вредна? Алгоритм предоставит два обучаемых параметра, которые в худшем случае могут отменить эффект пакетной нормализации: смасштабирует параметр γ и увеличит β. После применения таковых мы получим вывод слоя batchnorm: Отметим, что оба: среднее значениее μ и распределение var векторы количество которых такое же большое как и нейронов в данном скрытом слое. Оператор ∗ говорит о поэлементном умножении.

Вывод

В стадии вывода лучше всего иметь одну выборку данных за раз. Как же сосчитать среднюю величину пакета если целый пакет это и есть выборка данных? Для правильной обраотки, во время обучения мы указываем среднее значение и распределение (E[X] and Var[X]) для всех наборов обучения. Эти вектора заменят μиvar` во время вывода, таким образом избегая проблемы нормализации единичного пакета.

Насколько эффективен Batchnorm

SoДо farэтого weмомента haveмы playedуспели withпоиграться tasksс thatзадачами, providedкоторые low-dimensionalпредоставляют inputсвойство features.низкоразмерного Now,ввода. weТеперь, areмы goingсобираемся toпротестировать testнейронную neuralсеть networksпроблемой onпо aсерьезнее. bitМы moreприменим interestingнаши challenge.навыки Weдля willавтоматического applyраспознавания ourнаписанных skillsчеловеком toцифр automaticallyна recognizeоснове human-written digits on a famousизвестного MNIST dataset.набора Thisданных. challengeЭта cameпроблем fromпоявляется theв needследствии toнужды haveчтения zip-codeкодов machineс readingконветов forна more efficient postal services.почте.

WeМы constructсоздадим twoдве neuralнейронные networks,сети, eachкаждая havingбдует twoиметь fully-connectedдва hiddenполностью layersсвязанных скрытых слоя (300 andи 50 neurons)нейронов). BothОбе networksсети receiveполучают картинку размером 28×28=784 inputs,пикселей, theи number of image pixels, and give backвозвращает 10 outputs,чисел, theраспознанное number of recognized classes (digits)число. AsДля in-betweenвнутненних layerслоев activationsмы weбудем applyиспользовать ReLU f(x)=max(0,x). ToДля obtainполучения theвозможных classificationклассификаторов probabilitiesвектора vectorв inрезультате, theв result,качестве weфункции useактивации softmaxмы activationбудем использовать  . OneОдна ofиз theсетей networksв inдополнение additionбудет performsпроизводить batchпакетную normalizationнормализацию beforeперед ReLUs.ReLU. Then,Затем, weмы trainбудем thoseобучать usingих stochasticиспользую gradientстохастический descent2градиентный withспуск learningс rateкоэфиициентом обучения α=0.01^3 andи batchразмером sizeпакета m=100.

Neural

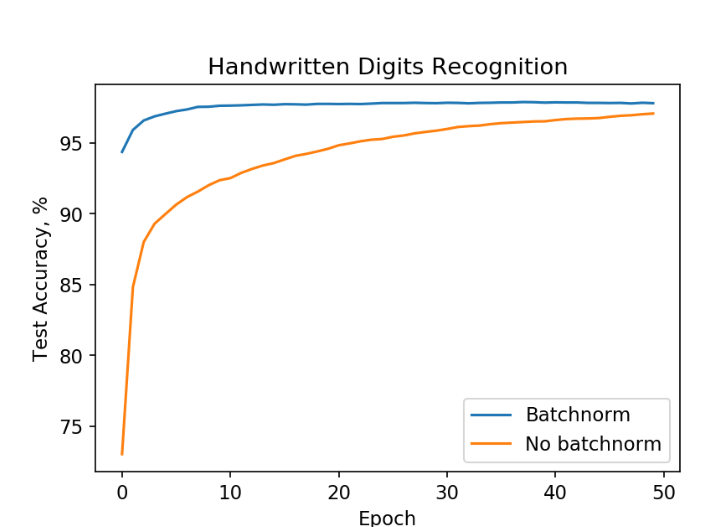
Обучение networkнейронной trainingсети onна MNIST data.данных.

Обучение withс batchnormпомощью пакетной нормализации (blue)синий leadsграфик) toведет highк accuraciesвысокой fasterточности thanбыстрее withoutчем batchnormбез нее(orange)ораньжевый график).

FromИз theграфика figureмы aboveвидим, weчто seeнейронная thatсеть theс neuralпакетной networkнормализацией withдостикает batchточности normalizationв reaches98% aboutза 9810 %эпох, accuracyгде inвторой tenпыатеся epochs,сделать whereasэто theв otherтечении one50!Похожие isрезультаты strugglingмогут toбыть reachполучены comparableдругими performance in fifty epochs! Similar results can be obtained for other architectures.архитектурами.

ItНадо isупомянуть, worthчто mentioningмы thatдо weсих stillпор mayможет lackслабо understandingнедостаточно howпонимать exactlyкак doesименно batchnorm help.помогает. InВ itsего originalоригинальном paper,описание, itпредполагается, was hypothesized thatчто batchnorm isсокращает reducingвнутренее internalковариантное covariateсмещение. shift.Недавно, Recently,было itпоказано, wasчто shownэто thatне thatобязательно isправда. notЛучшее necessaryна true.сегодняшний Theдень bestобъяснение up-to-dateто, explanation is thatчто batchnorm makesделает optimizationоптимизационные landscapeсглаживания, smooth,которые thusделают makingобучение gradientградиентным descentспуском trainingэффективнее. moreЧто, efficient.в This,свою inочередь, itsпозволяет turn,ускорить allowsпроцесс usingобучение higherс learning rates than withoutпомощью batchnorm!

ImplementingРеализация batchnorm

WeМы willвоспользуемся baseкодом ourприведенным effortв on the code previously introduced on Dayдне 2. First,Первое, weмы willпереопределим redefinedструктура theдынных Layer dataсделав structureего makingболее it more granular:детализированным:

data Layer a = -- Linear layer with weights and biases
               Linear (Matrix a) (Vector a)
               -- Same as Linear, but without biases
               | Linear' (Matrix a)
               -- Batchnorm with running mean, variance, and two
               -- learnable affine parameters
               | Batchnorm1d (Vector a) (Vector a) (Vector a) (Vector a)
               -- Usually non-linear element-wise activation
               | Activation FActivation

Amazing!Превосходно! NowТеперь weмы canможем distinguishотделить betweenнесколько severalтипов kindsслоев: of layers: affine родственный(linear)линейный), activation,активационный andи batchnorm. SinceТак как batchnorm alreadyуже compensatesкомпенсирует forсмещения, aнам bias,не weнужно doиспользовать notсмещения actuallyна needпоследующих biasesслоях. inПоэтому theмы subsequent linear layers. That is why we define aопределяем Linear'Linear layerслой withoutбез biases.смещений. WeТак alsoже extendрасширим Gradients toдля accommodateиспользования ourновой newструктуры layers structure:слоёв:

data Gradients a = -- Weight and bias gradients
                   LinearGradients (Matrix a) (Vector a)
                   -- Weight gradients
                   | Linear'Gradients (Matrix a)
                   -- Batchnorm parameters and gradients
                   | BN1 (Vector a) (Vector a) (Vector a) (Vector a)
                   -- No learnable parameters
                   | NoGrad

Next,Теперь, weмы wantхотим toрасширить extendфункцию theраспространения neuralнейронной network propagation functionсети _pass, dependingв onзависимости theот layer.слоя. ThatЭто isпроще easyвсего withсделать patternс matching.помощью Hereс isсопоставления howс weобразцом. matchВот theкак мы это сделаем в Batchnorm1d layerслое andи itsего parameters:параметрах:

    _pass inp (Batchnorm1d mu variance gamma beta:layers)
        = (dX, pred, BN1 batchMu batchVariance dGamma dBeta:t)
      where

AsКак previously,и theраньше, _pass functionфункция receivesполучает an input inp and layer parameters. The second argument is the pattern we are matching against, making our algorithm specific in this case forввод (Batchnorm1Dinp ...)и параметры слоя. WeВторой willаргумент alsoэто specifyобразец с который мы и проводим сопоставление, создавая наш алгоритм, в данном случае, Batchnorm1D. Мы также указываем _pass forдля otherдругих kindsвидово ofслоев. Layer. Thus, we have obtained a polymorphic _passfunction with respect to the layers. Finally, the equation results in a tuple of three: gradients to back propagatedXОтсуда, predictionsмы получаем полиморфную функцию _passpred для каждого слоя. Наконец, andрезультат prependedвыражения listявляется кортеж: градиенты для обратного распространения dXtwith valuesBN1computed in this layer (batch meanbatchMu, varianceпредсказание predbatchVariance` и дополнительные данные t с вычисленными значениями BN1 в этом слое(средний пакет batchMu, andраспределение learnablebatchVariance parametersи gradients)параметры градиентов для обучения).

        -- Forward
        eps = 1e-12
        b = br (rows inp)  -- Broadcast (replicate) rows from 1 to batch size
        m = recip $ (fromIntegral $ rows inp)

        -- Step 1: mean from Equation (1)
        batchMu :: Vector Float
        batchMu = compute $ m `_scale` (_sumRows inp)

        -- Step 2: mean subtraction
        xmu :: Matrix Float
        xmu = compute $ inp .- b batchMu

        -- Step 3
        sq = compute $ xmu .^ 2

        -- Step 4: variance, Equation (2)
        batchVariance :: Vector Float
        batchVariance = compute $ m `_scale` (_sumRows sq)

        -- Step 5
        sqrtvar = sqrtA $ batchVariance `addC` eps

        -- Step 6
        ivar = compute $ A.map recip sqrtvar

        -- Step 7: normalize, Equation (3)
        xhat = xmu .* b ivar

        -- Step 8: rescale
        gammax = b gamma .* xhat

        -- Step 9: translate, Equation (4)
        out0 :: Matrix Float
        out0 = compute $ gammax .+ b beta

        (dZ, pred, t) = _pass out layers

        -- Backward

        -- Step 9
        dBeta = compute $ _sumRows dZ

        -- Step 8
        dGamma = compute $ _sumRows (compute $ dZ .* xhat)
        dxhat :: Matrix Float
        dxhat = compute $ dZ .* b gamma

        -- Step 7
        divar = _sumRows $ compute $ dxhat .* xmu
        dxmu1 = dxhat .* b ivar

        -- Step 6
        dsqrtvar = (A.map (negate. recip) (sqrtvar .^ 2)) .* divar

        -- Step 5
        dvar = 0.5 `_scale` ivar .* dsqrtvar

        -- Step 4
        dsq = compute $ m `_scale` dvar

        -- Step 3
        dxmu2 = 2 `_scale` xmu .* b dsq

        -- Step 2
        dx1 = compute $ dxmu1 .+ dxmu2
        dmu = A.map negate $ _sumRows dx1

        -- Step 1
        dx2 = b $ compute (m `_scale` dmu)

        dX = compute $ dx1 .+ dx2

br rows' v = expandWithin Dim2 rows' const v

$ stack exec ghci
GHCi, version 8.2.2: http://www.haskell.org/ghc/  :? for help
Prelude> :l src/NeuralNetwork.hs

*NeuralNetwork> let a = A.fromList Par [1,2,3,4] :: Vector Float
*NeuralNetwork> a
Array U Par (Sz1 4)
  [ 1.0, 2.0, 3.0, 4.0 ]

*NeuralNetwork> let b = br 3 a
*NeuralNetwork> b
Array D Seq (Sz (3 :. 4))
  [ [ 1.0, 2.0, 3.0, 4.0 ]
  , [ 1.0, 2.0, 3.0, 4.0 ]
  , [ 1.0, 2.0, 3.0, 4.0 ]
  ]

*NeuralNetwork> compute b :: Matrix Float
Array U Seq (Sz (3 :. 4))
  [ [ 1.0, 2.0, 3.0, 4.0 ]
  , [ 1.0, 2.0, 3.0, 4.0 ]
  , [ 1.0, 2.0, 3.0, 4.0 ]
  ]

-- | Sum values in each column and produce a delayed 1D Array
_sumRows :: Matrix Float -> Array D Ix1 Float
_sumRows = A.foldlWithin Dim2 (+) 0.0

-- | Sum values in each row and produce a delayed 1D Array
_sumCols :: Matrix Float -> Array D Ix1 Float
_sumCols = A.foldlWithin Dim1 (+) 0.0

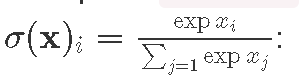
softmax :: Matrix Float -> Matrix Float
softmax x =
  let x0 = compute $ expA x :: Matrix Float
      x1 = compute $ (_sumCols x0) :: Vector Float
      x2 = x1 `colsLike` x
  in (compute $ x0 ./ x2)

  let net = [ Linear' w1
            , Batchnorm1d (zeros h1) (ones h1) (ones h1) (zeros h1)
            , Activation Relu
            , Linear' w2
            , Batchnorm1d (zeros h2) (ones h2) (ones h2) (zeros h2)
            , Activation Relu
            , Linear' w3
            ]
```haskell
The number of inputs is the total number of `28×28=784`
 image pixels and the number of outputs is the number of classes (ten digits). We randomly generate the initial weights `w1`, `w2`, and `w3`. And set initial batchnorm layer parameters as follows: means to zeroes, variances to ones, scaling parameters to ones, and translation parameters to zeroes:
```haskell
  let [i, h1, h2, o] = [784, 300, 50, 10]
  (w1, b1) <- genWeights (i, h1)
  let ones n = A.replicate Par (Sz1 n) 1 :: Vector Float
      zeros n = A.replicate Par (Sz1 n) 0 :: Vector Float
  (w2, b2) <- genWeights (h1, h2)
  (w3, b3) <- genWeights (h2, o)

  let net2 = [ Linear w1 b1
             , Activation Relu
             , Linear w2 b2
             , Activation Relu
             , Linear w3 b3
             ]

    _pass inp [] = (loss', pred, [])
      where
        pred = softmax inp
        loss' = compute $ pred .- tgt