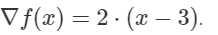День 1: Изучение Нейронной сети сложным путем.

Нейронная сеть - тема которая переодически появляется в моей жизни. Однажды, когда я был студентом, я был поглощен идеей построить интеллектуальную машину. Я провел пару бессонных ночей в думах. Я прочел несколько эссе проливающих свет на этот философский вопрос, среди которых самый видны, возможно, были записки Марвина Мински(Marvin Minsky). Как результат, я наткнулся на идею нейронной сети. Это был 2010 год, и глубокое обучение не было насколько популярным, как сейчас. Более того, ни кто не приложил много усилий, чтобы связать нейронную сеть в курсах математики или линейной алгебры. Даже ребята делая классическую оптимизацию и статистику иногда казались в затруднении слыша о нейронных сетях. Через несколько лет. я реализовал простую нейронную сеть с сигмоидной активацией как часть курса "принятия решения". В это же время я понял. что существующее положение нашего знания был до сих пор недостатком при создании "думающешго компьютера" на практике.

Это был 2012, конференция в Крыме, Украина где я присутствовал при разговоре с проф. Лореном Ларгером(Laurent Larger). Он объяснил как построить высоко-скоростное оборудование для распознавания речи используя лазер. Разговор меня вдохновил и годом позже я начал докторскую работу с целью разработать пластовые вычисления, рекурсивные нейронные сети реализуемые напрямую в железе. Наконец, теперь я использую нейронные сети как часть своей работы.

В это серии постов, я буду освещать некоторые интерсные детали проблемы решаемые с помощью нейронной сети. Я очень против повторяющихся усилий, поэтому я постараюсь обойти повторения сторон описанных много раз где-то еще. Для тех же, кто новичек в данной теме, вместо вступления в нейронные сети я буду ссылаться на главу 1.2 своей статьи: Theory and Modeling of Complex Nonlinear Delay Dynamics Applied to Neuromorphic Computing. Здесь, я всего лишь подведу итог, что нейронные сети были вдохновлены биологическими нейронами. Походя на своего билогического двойника, искуственный нейрон получает множество входных данных, проивзодит нелинейную транформацию, и делает вывод. Выражение ниже формализует тип поведения: 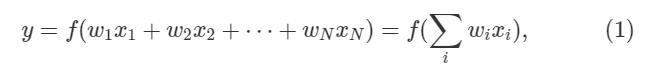где N это число входов x,w вес синапсиса, а y это результат. Удивительно, как может показаться, что в современной нейронной сети f может быть практически любой нелинейной. Эта нелинейная фнукия часто называемая функцией активации. Поздравляю, вы дошли до нейроной сети 1950 года.

Для продолжения чтения этой статьи, будут полезны, базовые математические знания, но не обязательно. Разрабатывать может любой у кого есть интуиция на тему нейронных сетей!

Слово о Haskell

Это серия постов практически иллюстрирует все концепты на языке программирования Haskell. Чтобы смотивировать вас на это, вот несколько вопросов и ответов, которые вы хотели знать.

Вопрос: Есть что, что делает Haskell практически лучше для нейронной сети или вы просто делаете это потому что вы предпочли Haskell?

Ответ: Неронные сети это просто "функциональный объекты". Сеть это просто большая композиция функци. А это естественная вещь для функционального языка.

Вопрос: Так как я абсолютный новичек в Haskell, хочу знать преимуства использвания Haskell перед python или другим языком?

Ответ: Вот основые преимущества:

Прост в понимании что делает ваша программа
Он хорош в переработке существующей кодовой базы.
Haskell направляет ваше мышление непосредственно к решению проблемы практическим путем.
Программы на Haskell быстры.

Вопрос: Мой недостаток знания Haskell будет мешать в чтении кода, но ваши примеры кода до сих пор имеют смысл для меня.

Ответ: Спасибо! Я нахожу Haskell интуитивно понятным при объяснени нейронных сеток.

Гадиентный спуск: Первый курс CS

Основная идея обучения нейронных сетей и глубокого обучения это логические оптимизационные методы известные как "Градиентный спуск". Для тех, кому сложно вспомнить первый курс, просто посмотрите видео объясняющее идею.

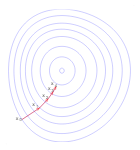
Как идея, простая как градиентный спуск может работать для нейронной сети? Пожалуй, нейронная сеть это всего лишь функция, сопоставляющая вход и выход. Сравнивая вывод нейронной сети с некоторым желаемым выводом, онам ожет получить другую функцию, известную как ошибочная функция. Это ошибочная фунцкия имеет конкретный ландшафт ошибок, как горы. Используя градиентный спуск, мы изменяем, нашу нейронную сеть так, будто мы спускаемся с этого ландафта. Далее, наша цель найти ошибку минимума. Ключевая идея метода оптимизации это, то что градиент ошибки дает нам направление в котором нам необходимо изменить нашу сеть. Похожим образом мы сможем спустится с холма покрытого густым туманом. В обоих случаях локальный градиент(наклон) нам доступен.

Градиентный спуск может быть описан формулойл: 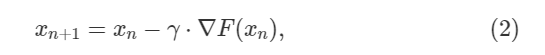где постоянная γ это то что называется скорость обучения в машинном обучении, таким образо количество обучения в одной итерации - n. В простом случае x скалярная величина. Метод градиентного спуска может быть применен в нескольких строках кода.

descend gradF iterN gamma x0 = take iterN (iterate step x0)
  where
    step x = x - gamma * gradF(x)

gradF_test x = 2 * (x - 3)

main = print (descend gradF_test iterN gamma 0.0)
  where
    iterN = 10
    gamma = 0.4

На выходе мы получим следующую последовательность:

[0.0,2.4000000000000004,2.88,2.976,2.9952,2.99904,2.999808,2.9999616,2.99999232,2.999998464]

Выходит. значение минимизации функции f(x) равно 3, то есть min f(x) = f(3) = (x-3)^2 = 0. А последовательность постепенно сходится к этому числу. Давайте посмотрим пристально на то, что делает код выше.

Линии 1-3: Мы определяем метод градиентного спуска, который пошагово применяет функцию step реализующую выражение 2. Мы предоставляем промежуточные результаты берущие первые iterN значения.
Линии 5: Предположим, мы хотим оптимизировать функцию f(x) = (x -3)^2. Тогда этот градиент gradF_test становится:

Линии 7-10: И вот, мы запустили наш градиентный спуск установив сколкрость обучения γ = 0.4.

Ключевой момент - понять как значение γ действует на сходимость. Когда γ слишком маленькое, алгоритм произведет множество итераций для схождения, однако если γ слишком большое, алгоритм никогда не сойдется. Я не пытаюсь показать простой путь как определить γ для заданной проблемы. Отсюда, должны использоваться различные значения γ. Вы можете поиграться с кодом выше и посмотреть что получается. Для примера вы можете попробовать различные значения γ, к примеру: 0.01, 0.1, 1.1. Метод применим ко множеству N. В далнейшем мы заменим gradF_test функцию скорей векторной, чем скалярной.

Части нейронной сети для задачи классификации

Растение Ирис