День 2: Что делают скрытые уровни?

На прошлом дне, мы ввели понятие обучения одноуровней нейронной сети. Сегодня мы узнаем преимущества многослойной нейронной сети, как правильно её организовывать и обучать.

Когда я обсуждаю нейронную сетку со студентами, которые только начали открывать технику машшиног обучения:

-Я сделал сетку распознавания цифр рукописного ввода. Но моя точность всего лишь Y

-Кажется это горазно меньше чем последнее слово техники, - размышляю я.

-Вот именно. Может быть прроблема в X?

Обычно X это не причина. Реальная причина должна быть более простая: вместо многослойной нейронной сети студент сделал однослойную нейронную сетку или её эквивалент. Эта сеть работает как линейный классификатор, следовательно она не может выучить не ленейные отношения между входом и желаемым выводом.

Так что такое многослойная нейронная сеть и как избежать ловушки с линейной классификацией.

Многослойная нейронная сеть.

Многослойная нейронная сеть, может быть описана как: где x и y это входные и выходные векторы соответственно,  - веса матриц и смещение векторов, и 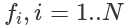 функции активации в i'том слое. Нелинейная функция активации f применяется поэлемментно.

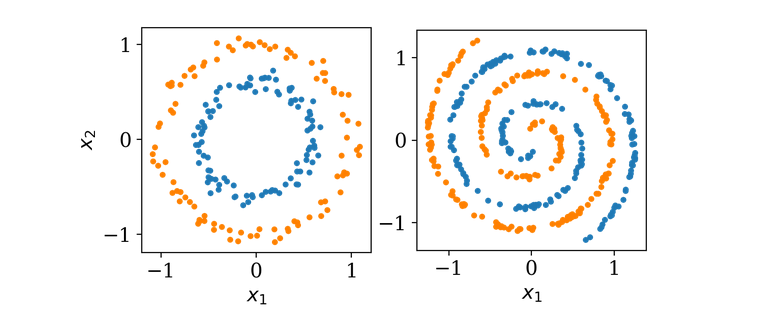
В качестве примера мы сегодня будем использовать двумерный набор данных как показано ниже.

Оба набора свойств двху классов изображена оранжевыми и синими точками. Цель обучения нейронной сети понять, как описать класс новой точки зная её координаты (x1, x2). Выхоит что это простое задание не может быть решено с помощью однослойной архитектуры, так как оди слой может вмещать только рисование прямой линии во входяем пространестве (x1,x2). Давайте добавим еще одни слой.

Двуслойная сеть.

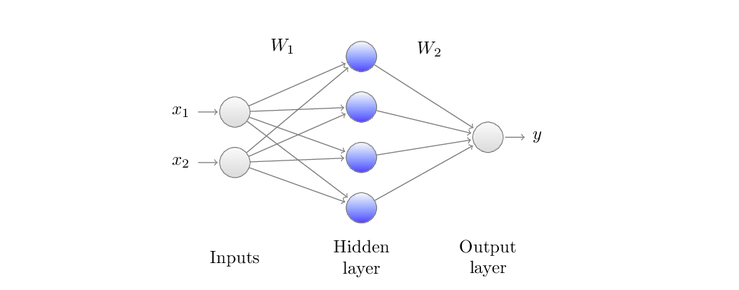
Ввод x1 и x2 - меремножаются весами матрицы W1, затем функция активации f1 применяется поэлементно. Наконец, данные преобразуются с помощью W2 и затем следующей функцией активации f2(не отображена) чтобы получить вывод y.

Картинка выше показывает однослойный скрытый нейронную архитектуру, которую мы будем взаимозамеяемо вызывать двух уровневую сетку: где f1(x) = max(0,x) так же известно как выпрямитель, будет первой активационной функцией и сигмоид f2(x)=σ(x)=[1+e^-1]^-1 - будет второй активационной функцией, которую вы уже видели в прошлой статье. Специфика сигмоида приводить вохдные данные к виду от 0 до 1. Этот вывод имеет тендецию быть ползеным в нашем случае где мы только имеет два класса: синие точки обозначенные как 0 и оранжевые точки как 1. Для минимизации функции потери во время обучения нейронной сети, мы будем использовать функция доичной перекресной энтропии.